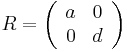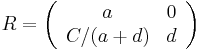Square root of a 2 by 2 matrix
A square root of a 2 by 2 matrix M is another 2 by 2 matrix R such that M = R2, where R2 stands for the matrix product of R with itself. In many cases, such a matrix R can be obtained by an explicit formula.[1]
Contents |
The general formula
Let
where A, B, C, and D may be real or complex numbers. Furthermore, let τ = A + D be the trace of M, and δ = AD - BC be its determinant. Let s be such that s2 = δ, and t be such that t2 = τ + 2s. That is,
Then, if t ≠ 0, a square root of M is
Indeed, the square of R is
Note that R may have complex entries even if M is a real matrix; this will be the case, in particular, if the determinant δ is negative.
Special cases of the formula
In general, the formula above will provide four distinct square roots R, one for each choice of signs for s and t. If the determinant δ is zero but the trace τ is nonzero, the formula will give only two distinct solutions. Ditto if δ is nonzero and τ2 = 4δ, in which case one of the choices for s will make the denominator t be zero.
The general formula above fails completely if δ and τ are both zero; that is, if D = −A and A2 = −BC. In this case, if M is the null matrix (with A = B = C = D = 0), then the null matrix is also a square root of M; othwerwise M has no square root.
Simplified formulas for special matrices
If M is diagonal (that is, B = C = 0), one can use the simplified formula
where a = ±√A and d = ±√D; which, depending on the sign choices, gives four, two, or one distinct matrices, if none of, only one of, or both A and D are zero, respectively.
If B is zero but A and D are not both zero, one can use
This formula will provide two solutions if A = D, and four otherwise. A similar formula can be used when C is zero but A and D are not both zero.
References
- ^ P. C. Somayya (1997), Root of a 2x2 Matrix, The Mathematics Education Vol.. XXXI. No. 1. Siwan, Bihar State. INDIA
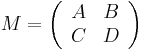
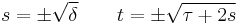
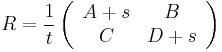
![\begin{array}{rcl}
R^2
&=&
\displaystyle \frac{1}{t^2}
\left( \begin{array}{cc} (A %2B s)^2 %2B B C & (A %2B s)B %2B B(D %2B s) \\ C(A %2B s) %2B (D %2B s)C & (D %2B s)^2 %2B B C \end{array}\right)\\[3ex]
{}
&=&
\displaystyle \frac{1}{A %2B D %2B 2 s}
\left( \begin{array}{cc} A(A %2B D %2B 2s) & (A %2B D %2B 2s)B \\ C(A %2B D %2B 2 s) & D(A %2B D %2B 2 s) \end{array}\right) \;=\;
M
\end{array}](/2012-wikipedia_en_all_nopic_01_2012/I/2f29af229059618e498796286cc7d492.png)